GEOMETRIA

DEPARTAMENTO DE ADSCRIPCION: DEPARTAMENTO DE MATEMATICAS
CARGA HORARIA SEMESTRAL: TEORIA: 60; PRACTICA: 0
CREDITOS: 9 TIPO: CURSO
AREA DE FORMACION: BASICA COMUN
PREREQUISITOS: NINGUNO

OBJETIVO GENERAL:

Aplicará la abstracción del álgebra a la geometría, así como los principios algebraicos a la geometría e integrar estos a las ciencias exactas y la ingeniería.
OBJETIVOS ESPECIFICOS:

El alumno identificará las curvas elementales en el plano en base a sus expresiones algebraicas. El alumno generalizará los conceptos de la geometría plana a la geometría del espacio. El alumno aplicará los conceptos de rotación, translación y cambio de coordenadas a las figuras elementales.
CONTENIDO TEMATICO:
1. INTRODUCCION


1.1 El plano Cartesiano
1.2 Coordenadas rectangulares
1.3 Puntos y segmentos de recta
1.4 Distancia entre dos puntos
1.5 Punto medio

2. ECUACIONES Y GRAFICAS


2.1 Variable dependiente, variable independiente
2.2 Ecuaciones y sus gráficas
2.3 Intersección de dos o más gráficas
2.4 Intersecciones de gráficas con los ejes
2.5 Simetría

3. LA LINEA RECTA


3.1 La ecuación general de la recta Ax+By+C=0
3.2 Pendiente
3.3 La forma y=mx+b
3.4 La forma punto pendiente y-y₁=m(x-x₁)
3.5 La forma x/a+y/b=1
3.6 Rectas paralelas y perpendiculares
3.7 Las rectas x=k, y=k

4. LA CIRCUNFERENCIA


4.1 Definición
4.2 Ecuación general de la circunferencia
4.3 Forma canónica
4.4 Determinar la ecuación de la circunferencia a partir de datos suficientes
4.5 Familias de circunferencias con un parámetro

5. PARABOLA


5.1 Definición
5.2 Forma general, forma canónica
5.3 Foco, vértice, directriz, excentricidad, lado recto
5.4 Parábolas horizontales y verticales
5.5 Propiedades geométricas de la parábola
5.6 Determinación de la ecuación de la parábola

6. LA ELIPSE


6.1 Definición
6.2 Ecuación gral. y ecuación canónica
6.3 Focos, centro, ejes, directrices, lado recto, excentricidad
6.4 Propiedades geométricas
6.5 Determinación de la forma y posición de la elipse

7. LA HIPERBOLA


7.1 Definición
7.2 Ecuación gral. y ecuación canónica
7.3 Focos, centro, ejes, directrices, asíntotas, lado recto, excentricidad
7.4 Propiedades geométricas
7.5 Determinación de la forma y posición de la hipérbola a partir de ciertos datos

8. SECCIONES CONICAS


8.1 Ecuación General de las cónicas
8.2 Casos particulares en base al valor del discriminante
8.3 Transformación de coordenadas
8.4 Traslación, rotación

9. COORDENADAS POLARES


9.1 Definiciones
9.2 Relación entra coordenadas polares y rectangulares
9.3 Ecuaciones polares de la recta, circunferencia y, en general, cónicas.
9.4 Ecuaciones polares de otras curvas

10. GEOMETRIA ANALITICA EN 3 DIMENSIONES


10.1 El plano
10.2 La línea recta
10.3 Curvas en el espacio
10.4 Superficies en general
10.5 Intersecciones
10.6 Conos, esferas y cilindros
10.7 Ecuaciones paramétricas
10.8 Coordenadas cilíndricas y esféricas


ESTRUCTURA CONCEPTUAL DE LA MATERIA:

BIBLIOGRAFIA BASICA:

• Steen & Ballou, GEOMETRIA ANALITICA, Publicaciones Cultural, México.

BIBLIOGRAFIA COMPLEMENTARIA:

• Reess & Sparks, ALGEBRA, Mc Graw-Hill, NY.
• W. Fleming & D. Vanverg, ALGEBRA LINEAL Y TRIGONOMETRIA CON GEOMETRIA ANALITICA, Prentice Hall Hispanoamericana, México.
• G. B. Thomas y R. L. Finney, CALCULO CON GEOMETRIA ANALITICA, Addison Wesley Iberoamericana, México.
• G. Fuller, W. L. Wilson y H. C. Miller, ALGEBRA UNIVERSITARIA, CECSA, México.
• E. P. Vance, ALGEBRA Y TRIGONOMETRIA, Fondo Educativo Interamericano. USA.
• Murdoch, GEOMETRIA ANALITICA CON VECTORES Y MATRICES, Noriega-Limusa, México.

MODALIDADES DE EVALUACION:

Tareas. Actividades complementarias. Exámenes parciales.
MATERIALES DE APOYO ACADEMICO:

Pizarrón y gis. Acetatos y transparencias. Guía de estudios. Notas de clase. Proyectos de investigación. Problemario
MODALIDADES DEL PROCESO ENSEÑANZA APRENDIZAJE:

La idea es que el curso no se convierta en una repetición de lo que se estudia en el bachillerato y tampoco se convierta en sesiones de resolución numérica de ejercicios sino que en base a la experiencia de los estudiantes se introduzcan los conceptos más importantes, poniendo énfasis en aquellos tópicos que tradicionalmente no son estudiados en el bachillerato. Se pretende que este curso sea un enlace entre la matemática del bachillerato y la matemática que se abordará en los cursos posteriores. En relación a la vinculación con casos prácticos o aplicaciones no se pretende que se lleve a cabo en este curso pues ellas serán abordadas en otras partes de cada plan de estudios y aquí lo que se busca es la comprensión y adquisición de los conocimientos matemáticos básicos para su posterior uso en las diferentes materias que integren cada plan de estudios.Se utilizaran los siguientes medios en el proceso de enseñanza: Exposición oral
Solución de problemas
Investigación bibliográfica
Realización de trabajos escritos por parte del alumno
Tareas
Exámenes parciales por escrito
CONOCIMIENTOS, APTITUDES, VALORES QUE EL ALUMNO DEBE ADQUIRIR CON BASE AL DESARROLLO DE LA UNIDAD:

El estudiante tendrá el dominio conceptual integro de los diferentes tópicos comprendidos en el estudio de la geometría analítica. Ampliará su conocimiento de los objetos geométricos dados por expresiones algebraicas. Desarrollará su intuición para reconocer objetos geométricos en espacios de dimensión mayor a 2.
CAMPO DE APLICACION PROFESIONAL:

El alumno será capaz de identificar claramente los modelos matemáticos básicos involucrados en los problemas que se le presenten durante el ejercicio de su profesión.  NOMBRE DE LA MATERIA: MT105 GEOMETRIA EUCLIDIANA
DEPARTAMENTO DE ADSCRIPCION: DEPARTAMENTO DE MATEMATICAS
CARGA HORARIA SEMESTRAL: TEORIA: 60 PRACTICA: 20
CREDITOS: 9
TIPO: CURSO-TALLER
AREA DE FORMACION: BASICA COMUN
PREREQUISITOS: NINGUNO

OBJETIVO GENERAL: Desarrollar la intuición y el rigor matemático en el estudiante por medio de la geometría euclidiana.
OBJETIVOS ESPECIFICOS: El alumno manejará formalmente los conceptos básicos de la geometría plana.;El alumno generalizará los conceptos de la geometría plana al espacio.El alumno comprenderá las relaciones y diferencias entre la geometría euclidiana y otras geometrías.
CONTENIDO TEMATICO:
1. CONCEPTOS FUNDAMENTALES (6 hrs.)
1.1 Objetivos de la Geometría (0.5 hr.)
1.2 Axiomas (0.5 hr.)
1.3 Postulados (1 hr.)
1.4 Primeras proposiciones de Euclides (1 hr.)
1.5 Listado de términos y conceptos básicos (1 hr.)
1.6 Paralelismo (0.5 hr.)
1.7 Perpendicularidad (0.5 hr.)
1.8 Métodos de demostración (1 hr.)

2. ANGULOS Y TRIANGULOS (6 hr.)
2.1 Elementos de ángulos (0.5 hr.)
2.2 Clasificación (0.5 hr.)
2.3 Unidades sexagesimales y radiales para medir ángulos (1 hr.)
2.4 Igualdad de ángulos (0.5 hr.)
2.5 Tipos de pares de ángulos (0.5 hr.)
2.6 Construcción de ángulos notables (0.5 hr.)
2.7 Reproducción de ángulos (0.5 hr.)
2.8 Definición de polígono y de triángulo (0.5 hr.)
2.9 Clasificación de triángulos (0.5 hr.)
2.10 Segmentos notables (1 hr.)

3. CONGRUENCIA DE TRIANGULOS (3 hrs.)
3.1 Diferencia entre congruencia e igualdad (1 hr.)
3.2 Criterios de congruencia de triángulos (1 hr.)
3.3 Teorema de congruencia (0.5 hr.)
3.4 Aplicaciones (0.5 hr.)

4. DESIGUALDAD DEL TRIANGULO (3 hrs.)
4.1 Teorema de la desigualdad del triángulo (1 hr.)
4.2 Teorema del ángulo externo (0.5 hr.)
4.3 Teorema de lados y ángulos opuestos en un triángulo (0.5 hr.)
4.4 Teoremas Asociados (0.5 hr.)
4.5 Aplicaciones (0.5 hr.)

5. PARALELAS (6 hrs.)
5.1 Ángulos alternos: internos y externos (0.5 hr.)
5.2 Ángulos correspondientes (0.5 hr.)
5.3 Definiciones usuales de paralelas (1 hr.)
5.4 Ángulos en paralelas (0.5 hr.)
5.5 Perpendicularidad (0.5 hr.)
5.6 El 5to. postulado de Euclides (1 hr.)
5.7 Teoremas asociados (0.5 hr.)
5.8 Teorema del punto medio del triángulo (0.5 hr.)
5.9 Aplicaciones (1 hr.)

6. CUADRILATEROS (4 hra.)
6.1 Clasificación de cuadriláteros (1 hr.)
6.2 Paralelogramos (1 hr.)
6.3 Trapecios (0.5 hr.)
6.4 Propiedades de los cuadriláteros (0.5 hr.)
6.5 Teoremas asociados (0.5 hr.)
6.6 Aplicaciones (0.5 hr.)

7. CIRCUNFERENCIA (9 hrs.)
7.1 Diferencias entre circunferencia y círculo (0.5 hr.)
7.2 Elementos Notables (0.5 hr.)
7.3 Arcos y ángulos centrales (1 hr.)
7.4 Longitud de Arco (0.5 hr.)
7.5 Tangentes y secante (0.5 hr.)
7.6 Teoremas Asociados (0.5 hr.)
7.7 Teorema del ángulo inscrito (0.5 hr.)
7.8 Ángulo inscrito en un diámetro (1 hr.)
7.9 Ángulo seminscrito (1 hr.)
7.10 La circunferencia inscrita, circunscrita y exinscrita en el triángulo (1 hr.)
7.11 Cuadriláteros inscritos (1 hr.)
7.12 Construcciones (1 hr.)

8. SEMEJANZA (6 hrs.)
8.1 Definición (0.5 hr.)
8.2 Semejanza de triángulos (0.5 hr.)
8.3 Propiedades de las proporciones (1 hr.)
8.4 Criterios de semejanza (1 hr.)
8.5 Teoremas asociados (1 hr.)
8.6 Teorema de Thales (1 hr.)
8.7 Teorema de Pitágoras (1 hr.)

9. SIMETRIA (2 hrs.)
9.1 Simetría puntual (0.5 hr.)
9.2 Simatría axial (0.5 hr.)
9.3 Construcciones (1 hr.)

10. ÁREAS (3 hrs.)
10.1 Superficies y áreas (0.5 hr.)
10.2 Concepción de área (0.5 hr.)
10.3 Área del cuadrado (0.25 hr.)
10.4 Área del rectángulo (0.25 hr.)
10.5 Área del triángulo (0.25 hr.)
10.6 Área de polígonos regulares e irregulares (0.25 hr.)
10.7 Área del círculo (0.5 hr.)
10.8 Área de sectores y seccciones del círculo (0.5 hr.)

11. GEOMETRIA DEL ESPACIO (6 hrs.)
11.1 Conceptos básicos (0.25 hr.)
11.2 Ángulos diedros (0.25 hr.)
11.3 Ángulos poliedros (0.25 hr.)
11.4 Vértices (0.25 hr.)
11.5 Aristas (0.25 hr.)
11.6 Caras (0.25 hr.)
11.7 Poliedros (0.25 hr.)
11.8 Poliedros regulares (0.5 hr.)
11.9 Prismas (0.25 hr.)
11.10 Palalelepípedos (0.25 hr.)
11.11 Pirámides (0.5 hr.)
11.12 Sólidos en revolución (0.5 hr.)
11.13 Superficies cilíndricas (0.5 hr.)
11.14 Superficies cónicas (0.5 hr.)
11.15 Los cuerpos redondos: cilindro, conos y esfera (0.25 hr.)
11.16 Las secciones cónicas (0.5 hr.)
11.17 Elementos Notables en la esfera (0.25 hr.)
11.18 Áreas y volúmenes (0.25 hr.)

12. TEMAS SELECTOS (3 hrs.)
12.1 Transformaciones del plano y del espacio (0.25 hr.)
12.2 ISometrías (0.25 hr.)
12.3 Homotecnia (0.25 hr.)
12.4 Inversión (0.25 hr.)
12.5 Geometrías no-euclideanas: Lobachevskiana, Riemanniana (0.25 hr.)
12.6 Geometría proyectiva (0.25 hr.)
12.7 Sistemas de axiomas e indefinibles (según Hilbert) (0.25 hr.)
12.8 Axiomas de pertenencia (0.25 hr.)
12.9 Axiomas de orden (0.25 hr.)
12.10 Axiomas de congruencia (0.25 hr.)
12.11 Axiomas de paralelas (0.25 hr.)
12.12 Axiomas de continuidad (0.25 hr.)


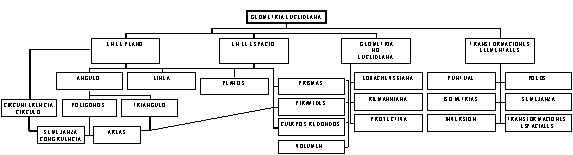
ESTRUCTURA CONCEPTUAL DE LA MATERIA:

BIBLIOGRAFIA BASICA:

• Wentworth y Smith, Geometría Plana y del Espacio, Ed. Porrua, México

BIBLIOGRAFIA COMPLEMENTARIA:

• D. Solow, Cómo entender y hacer demostraciones en Geometría, Limusa, México
• M. Issacs, Geometría Universitaria, Ed. Math.
• E. Filloy, Geometría, Grupo Editorial Iberoamerica, México

MODALIDADES DE EVALUACION: Tareas.Actividades complementarias.Exámenes parciales.
MATERIALES DE APOYO ACADEMICO: Pizarrón y gis. Acetatos y transparencias. Guía de estudios. Problemario. Notas de clase. Proyectos de investigación
MODALIDADES DEL PROCESO ENSEÑANZA APRENDIZAJE: La idea es que el curso se convierta en un buen ejemplo del rigor en las disciplinas deductivas, que no sea una repetición de lo que se estudia en el bachillerato y tampoco se convierta en sesiones de resolución numérica de ejercicios sino que en base a la experiencia de los estudiantes se introduzcan los conceptos más importantes, poniendo énfasis en aquellos tópicos que tradicionalmente no son estudiados en el bachillerato. Se pretende que este curso sea un enlace entre la matemática del bachillerato y la matemática que se abordará en los cursos posteriores.En relación a la vinculación con casos prácticos o aplicaciones no se pretende que se lleve a cabo en este curso pues ellas serán abordadas en otras partes de cada plan de estudios y aquí lo que se busca es la comprensión y adquisición de los conocimientos matemáticos básicos para su posterior uso en las diferentes materias que integren cada plan de estudios.Se utilizaran los siguientes medios en el proceso de enseñanza: Exposición oral
Solución de problemas
Investigación bibliográfica
Realización de trabajos escritos por parte del alumno
Tareas
Exámenes parciales por escrito

CONOCIMIENTOS, APTITUDES, VALORES QUE EL ALUMNO DEBE ADQUIRIR CON BASE AL DESARROLLO DE LA UNIDAD: El estudiante tendrá el dominio conceptual integro de los diferentes tópicos comprendidos en el estudio del geometría euclidiana. Además se pretende inculcar el gusto por el formalismo y la demostración, así como apreciar la belleza de los conceptos geométricos y la ingeniosa construcción en que se apoyan.
CAMPO DE APLICACION PROFESIONAL: El alumno será capaz de identificar claramente los modelos matemáticos básicos involucrados en los problemas que se le presenten durante el ejercicio de su profesión.